なぜ数学するのか?
Why Mathematics?
なぜ数学するのか?
この記事では、ポール・ロックハート著『測定』の抜粋を紹介し、数学を学ぶことについて一緒に考えたいと思います。この本は美しい表紙と親しみのある楽しい語り口調もさることながら、手書きの図形が随所に現れ、読書体験として幸福感を与えてくれるものとなっており、私のお気に入りの書物の一つです。
二部構成の本著の第一部『SIZE AND SHAPE』、49~50ページからの抜粋を、まずは原文の英語で読んでみましょう。
…. I want to address a serious question. Why are we doing this? What is the point of making up these imaginary shapes and then trying to measure them?
It’s certainly not for any practical purpose. In fact, these imaginary shapes are actually harder to measure than real ones. Measuring the diagonal of a rectangle requires insight and ingenuity; measuring the diagonal of a piece of paper is easy––just get out a ruler. There are no truths, no surprises, no philosophical problems at all. No, the issues we’re going to be dealing with have nothing to do with the real world in any way. For one thing, the patterns we will choose to measure will be chosen because they are beautiful and curious not because they are useful. People don’t do mathematics because it’s useful. They do it because it’s interesting.
But what’s so interesting about a bunch of measurements? Who cares what the length of some diagonal happens to be, or how much space some imaginary shape takes up? Those numbers are what they are. Does it really matter what?
Actually, I don’t think it does. The point of a measurement problem is not what the measurement is; it’s how to figure out what it is. The answer to the question about the diagonal of a square is not ; it’s the mosaic design. (At least that’s one possible answer!)
The solution to a math problem is not a number; it’s an argument, a proof. We’re trying to create these little poems of pure reason. Of course, like any other form of poetry, we want our work to be beautiful as well as meaningful. Mathematics is the art of explanation, and consequently, it is difficult, frustrating, and deeply satisfying.
It’s also a great philosophical exercise. We are capable of creating in our minds perfect imaginary objects, which then have perfect imaginary measurements. But can we get at them? There are truths out there. Do we have access to them? It’s really a question about the limits of the human mind. What can we know? This is the real question at the heart of every mathematics problem.
So the point of making these measurements is to see if we can. We do it because it’s a challenge and an adventure and because it’s fun. We do it because we’re curious, and we want to understand mathematical reality and the minds that can conceive it.

Measurement by Paul Lockhart
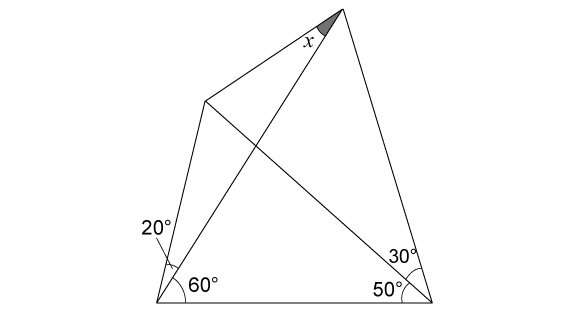
Langley’s Adventitious Angles
まず彼は、数学は面白いからやるのであって、役に立つということが目的ではない、ということを述べています。もちろん数学は役に立つのですが、私たち個人が数学をするという行為はそれ自体が芸術的かつ哲学的な楽しさと意義を持っています。
講師として高校生や中学生に得意科目や苦手科目について尋ねてみると、よくこんな表現を耳にします。「数学は答えが一つに決まっていてスッキリするから好きだが、国語は記述回答など答えがはっきり出ずぼんやりとしていてイマイチ掴めない」。確かに、難解な計算が正しくできた後に赤ペンで丸をつける清々しさは何物にも変え難いものがあります。しかし著者は、数学の「解決」というものは、その答えそのものではなく、そこへどのようにたどり着いたかである、と主張しているのです。初等幾何の有名な難題で、「ラングレーの問題」というものが存在します。
これも答えの数字に何か大きな価値があるというよりは、どうやってそれを出したのかという解法に驚きと美しさが宿っているといえます。小学生にこの問題を見せると、みんな躍起になって「15度!20度!」というふうに答えをあてずっぽうでも正解しようとするのに対し、高校生に見せると一通り頭を悩ませた後、「どうやって解くんですか」と聞いてくれるのが面白いです。
続けて著者は引用の中で、「我々はこうした純粋な論理の詩を創造しようとしているのである」と表現しており、こうした表現が私が彼の大ファンである所以でもあります。ピタゴラスの定理(直角三角形の直角を挟む二辺の平方の和は、斜辺の平方と等しい)も、定理それ自体はもちろん面白いのですが、真髄はどのように証明するかにあります。こうした数学の芸術性は、絵画にも通じるものがあると常々感じています。技術・想像力・創造力全てが集まって、脳が歓ぶ芸術活動は営まれるのです。
さらに、引用を読み進めていくと、数学は哲学的な営みである、ということも説明されていきます。「我々は何を知ることができるんだろう」という問いが数学の真髄だ、というわけです。私たちは頭の中に数学世界を作り出し、その世界に住む数字や形といったものたちをどこまで知ることができるのか、探検しているのです。
「なんで数学を勉強するのかわからない」
「受験勉強が辛くて、何が楽しいのかわからなくなってしまった」
「大人になって数学をまたやってみたいけれど、意義があるか不安である」
そうした向きには、ぜひ本著をお薦めしたいです。
美しいイラスト付きで、ふむふむと読み進められ、気がついたら数学の沼にハマっているでしょう。英文が苦手である、ということであれば、私が学習コーチとして一緒に精読し、学びの伴走者になることもできます。ぜひTankyuウェブサイトにてお問い合わせいただければ幸いです。
それでは、良き数学旅を!
2026/1/3(土)
デンチューリングほたる
Tankyu 学習コーチ
参照・引用元:
- 抜粋元の本:『測定』ポール・ロックハート(Measurement, Lockhart, Paul, 2012)
- 本の表紙画像:コロンビアマガジン(https://magazine.columbia.edu/article/book-review-measurement)
- ラングレーの問題図:算数星人ウェブサイト(https://sansu-seijin.jp/blog/archives/678)

